$$ \newcommand{\md}{\mathrm{d}} $$

1. Gibbs取样简介

Gibbs取样的核心在于写出多元变量的联合分布，然后根据 $p(X | Y)=\frac{p(X, Y)}{p(Y)}$ 写出各个变量的条件分布，之后使用已有变量样本，依次“抽取-更新”迭代：

$$ \begin{align*} \begin{split} 第n次迭代，变量样本为: x^{(n)} = (x_1^{(n)}, x_2^{(n)}, \dots, x_k^{(n)})^T \newline p(x_1 | x_2^{(n)}, x_3^{(n)}, \dots, x_k^{(n)})抽取变量即为x_1^{(n+1)} \newline p(x_2 | x_1^{(n+1)}, x_3^{(n)}, \dots, x_k^{(n)})抽取变量即为x_2^{(n+1)} \newline & \vdots \newline p(x_k | x_1^{(n+1)}, x_2^{(n+1)}, \dots, x_{k-1}^{(n+1)})抽取变量即为x_k^{(n+1)} \newline 生成新样本: x^{(n+1)} = (x_1^{(n+1)}, x_2^{(n+1)}, \dots, x_k^{(n+1)})^T \end{split} \end{align*} $$

当抽取足够多次时，计算目标函数$f(x)$的均值：

$$ \begin{align*} \begin{split} f_{mn} = \frac{1}{n-m}\sum_{i = m+1}^{n}f(x^{(i)}) \end{split} \end{align*} $$

2. 结合图模型提高抽样效率

在实际应用中，可以结合概率图模型提高抽样效率。具体原理是：对于随机变量$x_1, x_2, \dots, x_n$，条件概率：

$$ \begin{align} \begin{split} p(x_i|x_{\neg x_i}) &= p(x_i | x_1, \dots, x_{i-1}, x_{i+1}, \dots, x_n) \newline &= \frac{p(x_1, \dots, x_n)}{p(x_{\neg x_i})} \newline &= \frac{p(x_1, \dots, x_n)}{\int p(x_1, \dots, x_n) \md x_i} 或 \frac{p(x_1, \dots, x_n)}{\sum_{j = 1}^{k} p(x_1, \dots, x_i = j, x_n)} \newline & \propto p(x_1, \dots, x_n) \end{split} \label{eq:1} \end{align} $$

对于式$\eqref{eq:1}对于式$\eqref{eq:1}$：

• 分母可以看作常数。例如, $x_i$服从$k$个状态categorical分布，对于$\sum_{j=1}^{k} p(x_i = j | x_{\neg x_i}) = 1$，只需要求$p(x_1, \dots, x_i = j, \dots, x_n)$并标准化$\frac{p(x_1, \dots, x_i = j, \dots, x_n)}{\sum_{j = 1}^{k}p(x_1, \dots, x_i = j, \dots, x_n)}$即可。

• 分子中只考虑相互关联的随机变量。例如，《统计学习方法（第二版）》（李航 著）的图19.12中：$\alpha$指向$\theta$，$\theta$指向$z$与$y$，$x=(\alpha, \theta, z)$为模型参数或未观测数据，$y$为观测数据：

$$ \begin{align*} \begin{split} p(x | y) &= \frac{p(x, y)}{p(y)} \newline & \propto p(\alpha, \theta, z, y) \newline &= p(z, y | \theta, \alpha) p(\theta, \alpha) \newline &= p(z, y | \theta, \alpha) p(\theta | \alpha) p(\alpha) \newline &= p(z, y | \theta) p(\theta | \alpha) p(\alpha) \end{split} \end{align*} $$

所以，

$$ \begin{align*} \begin{split} p(\alpha_i|\alpha_{\neg i}, \theta, z, y) & \propto p(\alpha, \theta, z, y) \propto p(\theta | \alpha) p(\alpha) \newline p(\theta_i|\theta_{\neg i}, \alpha, z, y) & \propto p(\alpha, \theta, z, y) \propto p(z, y | \theta) p(\theta | \alpha) \newline p(z_i|z_{\neg i}, \alpha, \theta, y) & \propto p(\alpha, \theta, z, y) \propto p(z, y | \theta) \end{split} \end{align*} $$

3. 举例

3.1 gamma核和高斯核

一个有趣的例子是双变量$x, y$分布：

$$ \begin{align} \begin{split} p(x, y) = k x^2 e^{-xy^2 - y^2 + 2y - 4x}, x > 0, y \in \mathbb{R} \end{split} \label{eq:2} \end{align} $$

其中$k$为常数，保证$p(x, y)$积分为1。各变量的条件分布为：

$$ \begin{align*} \begin{split} p(y | x) &= N(\frac{1}{x+1}, \frac{1}{2(x+1)}) \newline p(x | y) &= Gamma(3, y^2+4) \end{split} \end{align*} $$

3.2 二元高斯分布

《统计学习方法（第二版）》（李航 著）给出一个二元高斯分布的例子，

$$ \begin{align*} \begin{split} p(x_1, x_2) &= N(0, \Sigma), \Sigma = \left[ \begin{matrix} 1 & \rho \\\ \rho & 1 \end{matrix} \right] \end{split} \end{align*} $$

各变量的条件分布为：

$$ \begin{align*} \begin{split} p(x_1 | x_2) &= N(\rho x_2, (1-\rho)^2) \newline p(x_2 | x_1) &= N(\rho x_1, (1-\rho)^2) \end{split} \end{align*} $$

当$\rho=0.5$时，模拟前$20$次取样如下（代码），第一个样本为$x_1 = -10, x_2 = -10$：

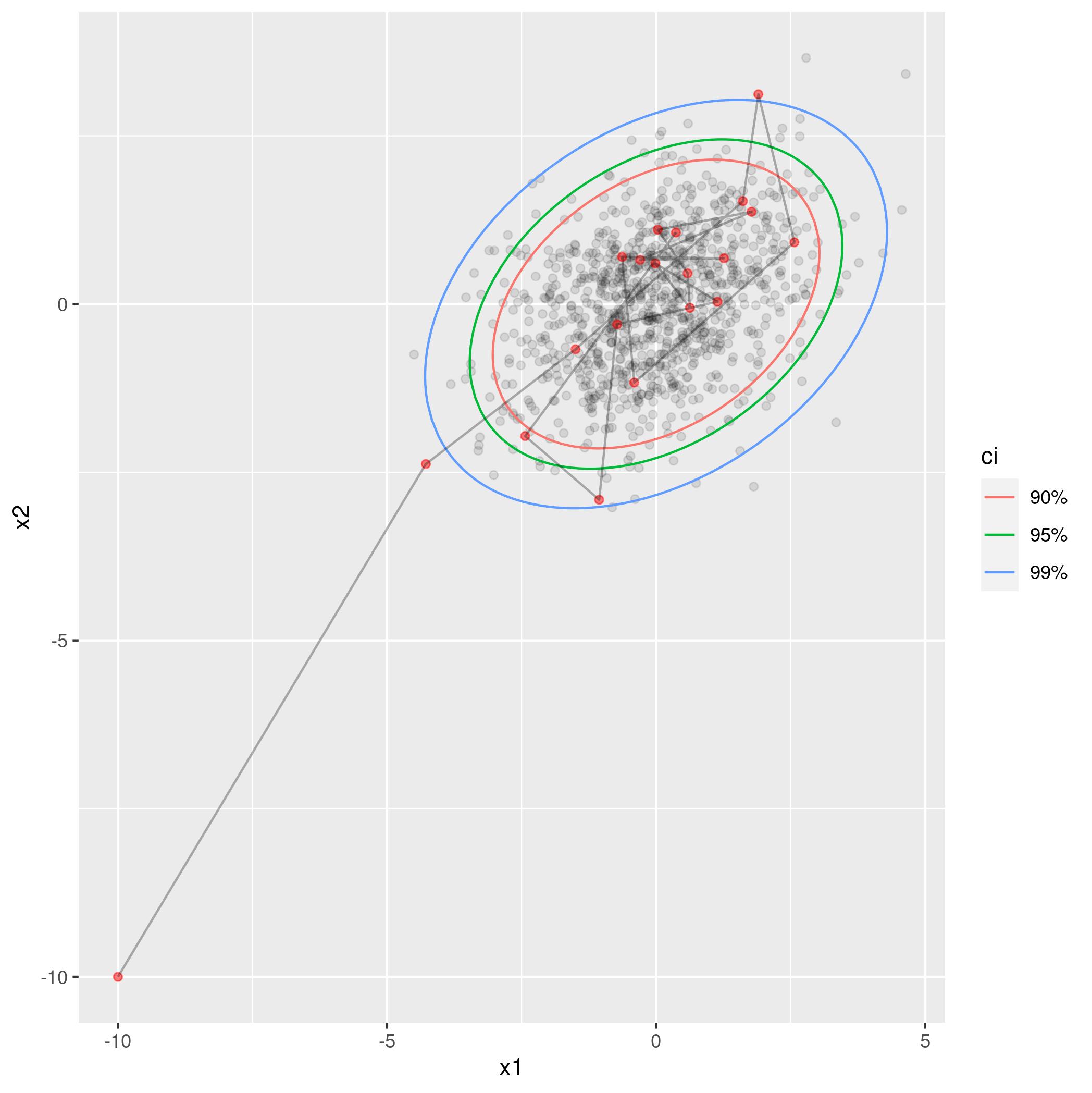
4. 一些积分

对于$\eqref{eq:2}$：

利用高斯积分

$$ \begin{align*} \begin{split} p(x) &= \int_{-\infty}^{+\infty } p(x, y) \md y \newline &= k x^2 e^{-4x}\int_{-\infty}^{+\infty } e^{-(x+1)y^2 + 2y} \md y \newline &= k x^2 e^{-4x} \sqrt{\frac{\pi}{x+1}} e^{\frac{1}{x+1}} \newline \end{split} \end{align*} $$

因此，

$$ \begin{align*} \begin{split} p(y | x) &= \frac{p(x, y)}{p(x)} \newline &= \frac{k x^2 e^{-4x} e^{{-(x+1)y^2 + 2y}}}{k x^2 e^{-4x} \sqrt{\frac{\pi}{x+1}} e^{\frac{1}{x+1}}} \newline &= \sqrt{\frac{x+1}{\pi}} e^{-(x+1)(y^2 - \frac{2y}{x+1} + \frac{1}{(x+1)^2})} \newline &= \sqrt{\frac{x+1}{\pi}} e^{-(x+1)(y - \frac{1}{x+1})^2} \end{split} \end{align*} $$

同理，

$$ \begin{align*} \begin{split} p(y) &= \int_{0}^{+\infty} p(x, y) \md x \newline &= k e^{-y^2+2y} \int_{0}^{+\infty} x^2 e^{-x(y^2+4)} \md x \end{split} \end{align*} $$

对于不定积分：

$$ \begin{align*} \begin{split} \int x^2 e^{-x(y^2+4)} \md x &= \frac{x^2 e^{-x(y^2+4)}}{-y^2 - 4} - \frac{2x e^{-x(y^2+4)}}{(-y^2 - 4)^2} + \frac{2e^{-x(y^2+4)}}{(-y^2 - 4)^3} + C \end{split} \end{align*} $$

因此，

$$ \begin{align*} \begin{split} p(y) &= k e^{-y^2+2y} \left(0 - \frac{2}{(-y^2 - 4)^3} \right) \newline &= k e^{-y^2+2y} \frac{2}{(y^2 + 4)^3} \end{split} \end{align*} $$

$$ \begin{align*} \begin{split} p(x | y) &= \frac{p(x, y)}{p(y)} \newline &= \frac{k e^{-y^2+2y} x^2 e^{-x(y^2+4)}}{ k e^{-y^2+2y} \frac{2}{(y^2 + 4)^3}} \newline &=\frac{(y^2 + 4)^3}{2} x^2 e^{-x(y^2+4)} \end{split} \end{align*} $$

参考资料

• MCMC and faster Gibbs Sampling using Rcpp

更新记录

2020年09月11日